Matemáticas Discretas.

CONJUNTO

1° Es la agrupación en un todo de objetos bien diferenciados en el la mente o en la intuición, por lo tanto estos objetos son bien determinados y diferenciados.

2° Es la reunión, agrupación o colección de elementos bien definidos que tienen una propiedad en común.

3° Un conjunto puede determinarse de 2 formas:

    - Por extensión: escribiendo dentro de una llave los nombres de los elementos del conjunto.

    - Por comprensión: escribiendo dentro de una lave una propiedad característica de los elementos del conjunto y solamente de ellos.

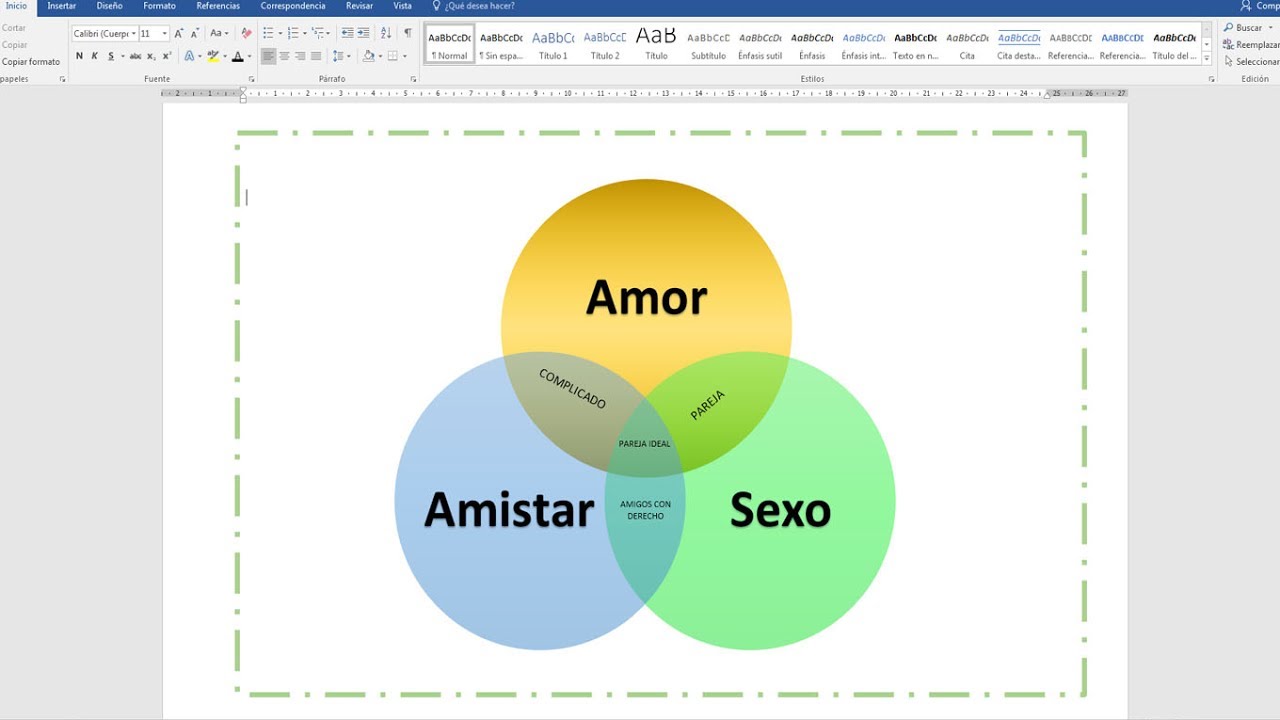
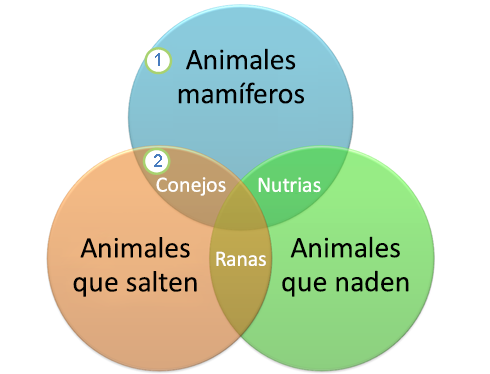
DIAGRAMA DE VENN

Un diagrama de Venn usa círculos que se superponen u otras figuras para ilustrar las relaciones lógicas entre dos o más conjuntos de elementos. A menudo, se utilizan para organizar cosas de forma gráfica, destacando en qué se parecen y difieren los elementos. Los diagramas de Venn, también denominados "diagramas de conjunto" o "diagramas lógicos", se usan amplia mente en las áreas de matemática, estadística, lógica, enseñanza, lingüística, informática y negocios.Los diagramas de Venn permiten a los usuarios visualizar los datos de forma clara y con gran alcance y, por este motivo, se utilizan comúnmente en presentaciones e informes.

OPERACIONES BÁSICAS DE CONJUNTOS

-NOMBRE: 

• Pertenencia. La relación relativa a conjuntos más básica es la relación de pertenencia. Dado un elemento x, éste puede o no pertenecer a un conjunto dado A. Esto se indica como:

${\displaystyle x\in A\quad \longrightarrow }$ x pertenece a A.

${\displaystyle x\notin A\quad \longrightarrow }$ x no pertenece a A.

• Igualdad. Dos conjuntos son iguales si y sólo si tienen los mismos elementos. Este principio, denominado principio de extensionalidad establece el hecho de que un conjunto queda definido únicamente por sus elementos

${\displaystyle A=B\quad \longrightarrow }$ A es igual a B.

${\displaystyle A\neq B\quad \longrightarrow }$ A no es igual a B.

• Inclusión. Dado un conjunto A, cualquier subcolección B de sus elementos es un subconjunto de A, y se indica como:

${\displaystyle A\subseteq B\quad \longrightarrow }$A es un subconjunto de B.

${\displaystyle A\nsubseteq B\quad \longrightarrow }$ A no es subconjunto de B.

-DEFINICIÓN:En matemáticas, un conjunto es una colección de objetos considerada como un objeto en sí. Los objetos de la colección pueden ser cualquier cosa: personas, números, colores, letras, figuras, etc. Cada uno de los objetos en la colección es un elemento o miembro del conjunto.

Un conjunto suele definirse mediante una propiedad que todos sus elementos poseen. 

Un conjunto queda definido únicamente por sus miembros y por nada más. En particular el orden en el que se representen estos es irrelevante. Además, cada elemento puede aparecer de manera idéntica una sola vez, esto es, no puede haber elementos totalmente idénticos repetidos.

Los conjuntos pueden ser finitos o infinitos. El conjunto de los número naturales es infinito, pero el conjunto de los planetas en el Sistema Solar es finito (tiene ocho elementos). Además, con los conjuntos pueden combinarse mediante operaciones, de manera similar a las operaciones con números.

-SIMBOLOGÍA:

-Operación con Diagrama de Venn

1:    A = {1, 2, 3, 4, 5}, B = {2, 3}, C = {3, 4}, D = {5, 6}. 

2:  A = {1; 2; 3; 4; 6; 12}

B = {1; 3; 5; 15}
U = {1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12; 13; 14; 15; 16}

                                                                                                                                                                                        Tablas de verdad, ejemplos:

Negación: El valor de verdad de la negación es el contrario de la proposición negada.

P	¬ P
1	0
0	1

 

Disyunción: La disyunción solamente es falsa si lo son sus dos componentes.

P	Q	P∨ Q
1	1	1
1	0	1
0	1	1
0	0	0

 

Conjunción: Solamente si las componentes de la conjunción son ciertas, la conjunción es cierta.

P	Q	P ∧ Q
1	1	1
1	0	0
0	1	0
0	0	0

Diferencia entre tablas de verdad y los mapas de Karnaugh:

En la tabla de la verdad tienes todas las salidas que existen para toda combinación posible en la entrada. 

En cambio en Karnaugh tienes esa misma información pero ordenada de forma tal que podes hallar la función lógica simplificada que representa al circuito. Karnaugh sirve para eso...simplificar las expresiones. 
Con esto te ahorras de hacer cálculos para simplificar expresiones booleana.